Profil des Bachelorstudiengangs Mathematik
Der Bachelorstudiengang Mathematik ist konsekutiv ausgerichtet und hat ein forschungsorientiertes Profil. Er führt zu einem ersten berufsqualifizierenden Studienabschluss. Die Regelstudienzeit beträgt 6 Semester (3 Jahre) mit Beginn zum Wintersemester im Oktober. Ein Beginn zum Sommersemester im April ist nur möglich, wenn bereits anrechenbare Leistungen vorliegen. Die Unterrichtssprache ist Deutsch.
Von Beginn des Studiums an profitieren Sie von der mathematischen Breite an der Universität Bonn. Die einzigartige Zusammenstellung der Grundvorlesungen vermittelt aufeinander abgestimmt ein umfassendes Basiswissen. Im weiteren Studienverlauf steht Ihnen eine große Vielfalt an Spezialisierungen aus der reinen und angewandten Mathematik zur Auswahl. Nebenfach und Praktikum im Bachelorprogramm geben die Gelegenheit, mathematische Kenntnisse und Methoden anzuwenden.
Die Lehrveranstaltungen des Bachelorstudiengangs Mathematik werden in Form von Modulen (Vorlesungen, Seminare und Praktika) angeboten. Sie dauern jeweils ein Semester und werden mit einer Prüfung abgeschlossen.
Studienprogramm
Die sechs Vorlesungspflichtmodule werden standardmäßig im ersten Studienjahr absolviert. Mit der Entwicklung ihrer jeweils spezifischen Lehrinhalte schaffen die drei Vorlesungen in ihrer Kombination die Grundlage für alle mathematischen Theorien und Anwendungen. Anhand von analytischen, algebraischen und algorithmischen Methoden werden die Grundtechniken des mathematischen Arbeitens vermittelt.
- Analysis I und II: Ausgehend von der Schulmathematik wird die Differential- und Integralrechnung in ein und mehreren Raumdimensionen systematisch entwickelt. Auf natürliche Weise eröffnen sich zahlreiche neue Fragestellungen und Gebiete wie Differentialgleichungen, Funktionenräume oder Differentialgeometrie.
- Lineare Algebra I und II: Der Begriff des Vektors wird abstrahiert und daraus eine algebraische Theorie der allgemeinen Vektorräume formal aufgebaut. Dabei werden die linearen Abbildungen auf Vektorräumen klassifiziert und die Vektoren- und Matrizenrechnung entwickelt.
- Algorithmische Mathematik I und II: Diskrete Mathematik, Numerik und Stochastik sind mathematische Gebiete, deren Anwendung auf den Einsatz von Algorithmen und Computern zurückgreift. Die Vorlesung bietet eine Einführung in diese Gebiete und die damit verbundenen Algorithmen inklusive der Programmierung.
Ab dem dritten Semester stehen ein- und weiterführende Vorlesungen auf dem Programm. Diese gehören jeweils zu einem der sechs mathematischen Studienbereiche A-F. Insgesamt werden mindestens sechs Vorlesungen benötigt, wobei vier Bereiche abgedeckt werden müssen. Zur Orientierung sollten im 3. Studiensemester Vorlesungen in drei verschiedenen Bereichen gehört werden.
Aus jedem der 6 Bereiche werden pro Semester meist eine einführende (V2..) und mindestens eine weiterführende Vorlesung (V3..) angeboten.
Für den erfolgreichen Studienabschluss müssen Sie zwei Bereiche mit jeweils mindestens 18 LP und zwei weitere mit mindestens 9 LP aus Vorlesungsmodulen abdecken. Demnach müssen Sie je zwei Vorlesungen aus zwei sowie je eine Vorlesung aus zwei weiteren der sechs Studienbereiche erfolgreich abschließen.
Seminare vertiefen und ergänzen die Vorlesungen. Im Studienprogramm ist mindestens ein Hauptseminar vorgeschrieben. In einem Seminar hält jede/r TeilnehmerIn einen Vortrag zu einem vorher mit dem Dozenten oder der Dozentin festgelegten Thema. Dieser Vortrag wird als Prüfungsleistung benotet. In Seminaren soll die Diskussion über mathematische Themen eingeübt werden, daher gilt Anwesenheitspflicht.
In jedem Sommersemester werden mehrere einführende Seminare (S1G1) angeboten. Sie sollen einen Einblick in die selbständige Aufbereitung und Präsentation mathematischer Zusammenhänge vermitteln. Die einführenden Seminare gehören zum Wahlpflichtprogramm.
Das verpflichtende Hauptseminar wird in der Regel im 3. oder 4. Semester absolviert. Häufig stammt es aus dem Bereich, in dem dann auch die Bachelorarbeit geschrieben wird. Es können auch mehrere (verschiedene) Hauptseminare besucht werden.
Zum Pflichtprogramm des Bachelorstudiengangs gehört weiterhin eines von mehreren möglichen Praktika. Dabei soll die theoretische und abstrakte Beschäftigung mit mathematischem Stoff durch praktische Aufgaben und Anwendungen ergänzt sowie ein Einblick in die berufliche Tätigkeit von MathematikerInnen vermittelt werden. Ein Praktikum wird für das 4. oder 5. Fachsemester empfohlen.
Zur Wahl stehen
- ein Tutorenpraktikum, bei dem Sie eine Übungsgruppe zu einer Vorlesung leiten und anschließend Ihre didaktische Tätigkeit in einem Portfolio reflektieren,
- ein Industriepraktikum, bei dem Sie eine praktische Tätigkeit mit mathematischem Bezug in einer selbst ausgesuchten Firma absolvieren,
- ein Programmierpraktikum:
- Praktikum Mathematische Logik
- Programmierpraktikum Diskrete Optimierung
- Programmierpraktikum Numerische Simulation.
Ein Nebenfach ist fester Bestandteil des Bachelorstudiums. Die drei Standardnebenfächer im Bachelorstudiengang Mathematik sind Physik, Informatik und Volkswirtschaftslehre. Weitere Fächer sind ggf. auf Antrag möglich. In dem gewählten Fach müssen mindestens 24 Leistungspunkte erworben werden. Es wird empfohlen, eine erste einführende Nebenfachvorlesung im 2. oder 3. Semester zu belegen.
- Ein von den drei o.g. Standardfächern abweichendes ("außerordentliches") Nebenfach muss vom Bachelor-Master-Büro Mathematik genehmigt werden, bevor Sie darin Prüfungen ablegen können.
- Generell gelten für alle Module Ihres Nebenfachs die Regeln der Lehreinheit, die das Modul anbietet, nicht die der Mathematik! Somit unterscheiden sich die Anmeldefristen und -modalitäten für Nebenfachmodule von Fach zu Fach und von denen der Mathematik.
Weitere Informationen finden Sie unter Nebenfach, insbesondere zur Genehmigung außerordentlicher Nebenfächer.
Der Studiengang schließt mit zwei Pflichtmodulen, der Bachelorarbeit und dem Begleitseminar zur Bachelorarbeit, ab. Damit sollen Sie zeigen, dass Sie wissenschaftliche Methoden anwenden und mathematische Sachverhalte angemessen darstellen können. Das Vertiefungsgebiet für die Bachelorarbeit sollte am besten zu Beginn des 5. Fachsemesters gewählt werden. Die Bearbeitungszeit beträgt 5 Monate.
In der Regel beginnt man am Ende des 5. Fachsemesters mit der Bachelorarbeit. Es empfiehlt sich, zur Vorbereitung darauf
- (weitere) Wahlpflichtvorlesungen Ihres gewählten Vertiefungsbereichs zu hören,
- ein (zweites) Hauptseminar in Ihrem Vertiefungsgebiet zu absolvieren,
- früh genug einen Dozenten/eine Dozentin anzusprechen, um ein Thema für die Arbeit festzulegen.
In Vorbereitung auf die Bachelorarbeit muss eine zweistündige Schulungsveranstaltung zur fachspezifischen Literaturrecherche besucht werden. Dies ist eine Studienleistung zum Bachelorarbeits-Begleitseminar, ohne die das Begleitseminar nicht bestanden werden kann.
Im Bachelorstudiengang Mathematik besteht der Pflichtbereich aus
- den sechs Vorlesungspflichtmodulen
- der Bachelorarbeit und dem Begleitseminar.
Wenn Sie die Pflichtvorlesungen bestanden haben, eröffnen sich viele Wahlmöglichkeiten. Bitte beachten Sie unsere Hinweise zur
Die Bachelorprüfung ist bestanden, sobald die folgenden Anforderungen erfüllt sind:
Leistungspunkte (LP):
- Die sechs Grundvorlesungen sind bestanden.
6 · 9 = 54 LP
- Sechs Vorlesungsmodule aus den Bereichen A bis F sind bestanden, wobei zwei verschiedene Bereiche mit je zwei Vorlesungen und zwei weitere mit je einer Vorlesung abgedeckt sind.
6 · 9 = 54 LP
- Ein Hauptseminar ist bestanden.
6 LP
- Ein Praktikum ist bestanden.
9 LP
- Ein zulässiges Nebenfach ist bestanden.
Werden mehr als 24 LP erbracht, so zählen alle überschüssigen LP für den freien Wahlpflichtbereich.
24 LP
- Die Bachelorarbeit und das Begleitseminar zur Bachelorarbeit sind bestanden.
12 + 6 = 18 LP
- Weitere Module des freien Wahlpflichtbereichs sind bestanden. Dabei dürfen bis zu 6 LP aus Modulen anderer Studiengänge der Universität Bonn erbracht werden, die keine inhaltliche Nähe zu Mathematikmodulen aufweisen.
15 LP
- Insgesamt wurden 180 Leistungspunkte erworben.
180 LP
In der Prüfungsordnung sind alle Regelungen für Ihren Studiengang rechtsverbindlich zusammengestellt. Bitte achten Sie auf das Datum der für Sie geltenden Prüfungsordnung.
Das Modulhandbuch führt die Module auf, die zu Ihrem Studiengang gehören oder darin zulässig sind. Hier finden Sie Angaben zum Inhalt der Module, zu den Zulassungsvoraussetzungen, zu Art und Umfang der Prüfungen sowie zu den Leistungspunkten, mit denen das Modul bewertet ist.
Ausgelaufene Prüfungsordnungen finden Sie in unserem Dokumentenarchiv.
Beispielstudienpläne
Die Graphik zeigt ein allgemeines Studienschema. Der genaue Studienplan hängt von der Wahl des Nebenfaches, des Vertiefungsgebietes, des Praktikums und natürlich von Ihrer persönlichen Motivation und Begabung ab. Daher haben wir einige konkrete Beispielstudienpläne mit verschiedenen Parametern für Sie zusammengestellt. Bitte beachten Sie, dass sich hierbei die Semesterangaben auf die Regelstudienzeit beziehen. Andere Studienverläufe nach individuellem Bedarf sind selbstverständlich möglich.
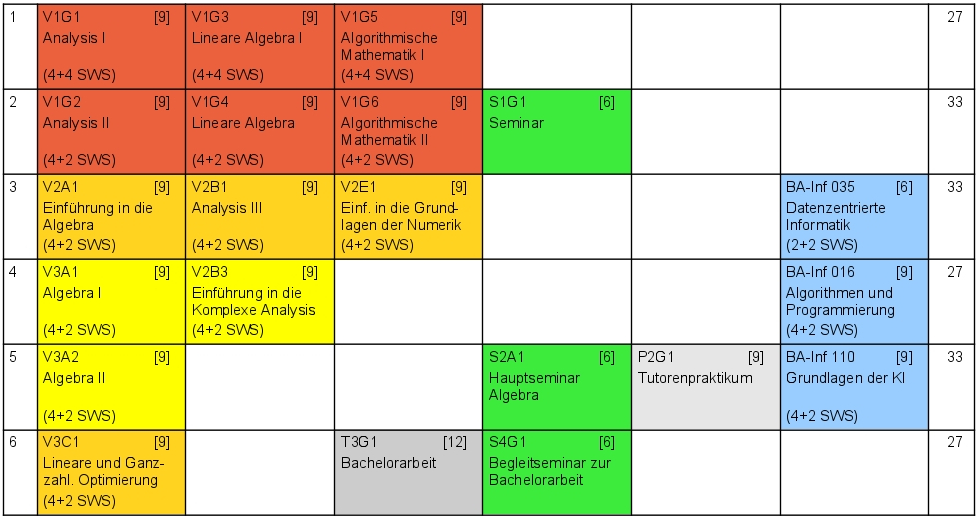
Die Zeilennummern geben die fortlaufende Semesterzahl an. Zwischen den Spalten besteht kein Unterschied, die Farben haben jedoch folgende Bedeutungen:
- rot = Grundvorlesungen
- orange = einführende Vorlesungen (Bereiche A bis F)
- gelb = weiterführende Vorlesungen (Bereiche A bis F)
- hellgrün / grün = Seminare
- hellgrau = Praktikum
- blau = Nebenfach
- dunkelgrau = Bachelorarbeit
Die Zahlen in den eckigen Klammern repräsentieren die Anzahl der Leistungspunkte (LP), die Zahlen in den runden Klammern die Semesterwochenstunden (SWS), d.h. die wöchentlichen Anwesenheitsstunden.
Studienbeginn
- Was muss ich zu Beginn des Studiums beachten?
- Welche Herausforderungen erwarten mich in der Bonner Mathematik?
- Welche Möglichkeiten der Unterstützung habe ich für den Studieneinstieg?
Organisation im Studium
- Wie kann ich an einer Lehrveranstaltung teilnehmen?
- Wie melde ich mich zu einer Prüfung an?
- Welche wichtigen Fristen und Termine darf ich nicht verpassen?
- Was tue ich, wenn ich am Tag der Prüfung krank bin?
Externe Praktika und Jobs
- Wo kann ich ein Praktikum außerhalb der Universität absolvieren?
- Wie kann ich mich auf den Berufseinstieg vorbereiten?
- Wo kann ich mit Arbeitgebern in Kontakt kommen und mögliche Jobangebote finden?
Kontakt